题目
题目背景
某个局域网内有n(n<=100)台计算机,由于搭建局域网时工作人员的疏忽,现在局域网内的连接形成了回路,我们知道如果局域网形成回路那么数据将不停的在回路内传输,造成网络卡的现象。因为连接计算机的网线本身不同,所以有一些连线不是很畅通,我们用f(i,j)表示i,j之间连接的畅通程度,f(i,j)值越小表示i,j之间连接越通畅,f(i,j)为0表示i,j之间无网线连接。
题目描述
需要解决回路问题,我们将除去一些连线,使得网络中没有回路,并且被除去网线的Σf(i,j)最大,请求出这个最大值。
输入格式
第一行两个正整数n k
接下来的k行每行三个正整数i j m表示i,j两台计算机之间有网线联通,通畅程度为m。
输出格式
一个正整数,Σf(i,j)的最大值。
输入样例
1 | 5 5 |
输出样例
1 | 8 |
说明
f(i,j)<=1000
题解
这里可以采用存边的方法存储图,再用克鲁斯卡尔按边求出最小生成树,把这些边标记起来,再把没有标记过的相加,这样做的好处是避免数据溢出(当然你也可以开长整型)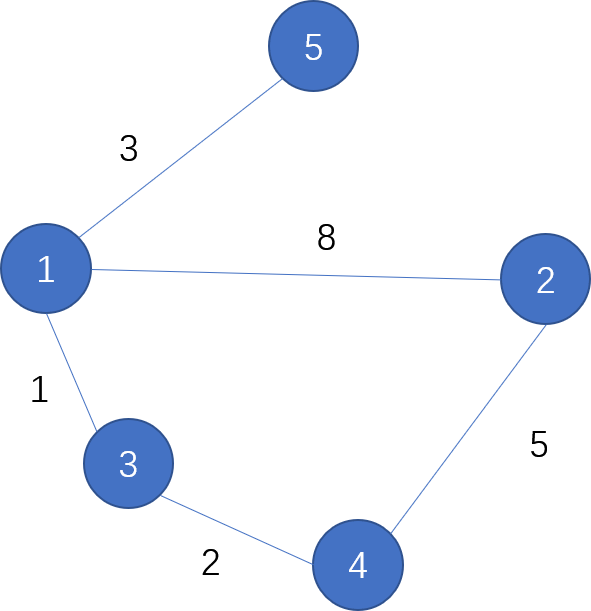
代码
1 |
|